Moment-generating function
In probability theory and statistics, the moment-generati
wherever this expectation exists. The moment-generati
For vector-valued random variables X with real components, the moment-generati
where t is a vector and 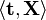 is the dot product.
is the dot product.
Provided the moment-generati
If X has a continuous probability density function f(x) then the moment generating function is given by
where mi is the ith moment. MX( − t) is just the two-sided Laplace transform of f(x).
Regardless of whether the probability distribution is continuous or not, the moment-generati
where F is the cumulative distribution function.
If X1, X2, ..., Xn is a sequence of independent (and not necessarily identically distributed) random variables, and
where the ai are constants, then the probability density function for Sn is the convolution of the probability density functions of each of the Xi and the moment-generati
Related to the moment-generati
The cumulant-generating function is the logarithm of the moment-generati

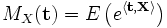


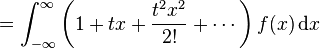




No comments:
Post a Comment