The one-sample KS test compares the empirical distribution function with the cumulative distribution function specified by the null hypothesis. The main applications are testing goodness of fit with the normal and uniform distributions. For normality testing, minor improvements made by Lilliefors lead to the Lilliefors test. In general the Shapiro-Wilk test or Anderson-Darlin
1. One-Sample
1. Introduction
A test for goodness of fit usually involves examining a random sample from some unknown distribution in order to test the null hypothesis that the unknown distribution function is in fact a known, specified function.
We usually use Kolmogorov-Smirnov test to check the normality assumption in Analysis of Variance.
A random sample X1,X2, . . . , Xn is drawn from some population and is compared with F∗(x) in some way to see if it is reasonable to say that F∗(x) is the true distribution function of the random sample.
One logical way of comparing the random sample with F∗(x) is by means of the empirical distribution function S(x)
2. Definition
Let X1,X2, . . . , Xn be a random sample. The empirical distribution function S(x) is a function of x, which equals the fraction of Xis that are less than or equal to x for each x, −∞<x<∞, i.e:
The empirical distribution function S(x) is useful as an estimator of F(x), the unknown distribution function of the Xis.
We can compare the empirical distribution function S(x) with hypothesized distribution function F∗(x) to see if there is good agreement.
One of the simplest measures is the largest distance between the two functions S(x) and F∗(x), measured in a vertical direction. This is the statistic suggested by Kolmogorov (1933).
3. Kolmogorov-Smirnov test (K-S test)
The data consist of a random sample X1,X2, . . . , Xn of size n associated with some unknown distribution function,denoted by F(x).
The sample is a random sample.
Let S(x) be the empirical distribution function based on the random sample X1,X2, . . . , Xn. Let F∗(x) be a completely specified hypothesized distribution function.
Let the test statistic T be the greatest (denoted by ”sup” for supremum) vertical distance between S(x) and F∗(x).In symbols we say
For testing
H0 : F(x) = F∗(x) for all x from −∞ to ∞
H1 : F(x) <> F∗(x) for at least one value of x
If T exceeds the 1-αquantile as given by Table then we reject H0 at the level of significance α. The approximate p-value can be found by interpolation in Table.
4. Example
A random sample of size 10 is obtained: X1 = 0.621,X2 = 0.503,X3 =0.203,X4 = 0.477,X5 = 0.710,X6 = 0.581,X7 = 0.329,X8 = 0.480,X9 =0.554,X10 = 0.382.The null hypothesis is that the distribution function is the uniform distribution function whose graph in Figure 1.The mathematical expression for the hypothesized distribution function is

Formally, the hypotheses are given by
H0 : F(x) = F∗(x) for all x from −∞ to ∞
H1 : F(x) _= F∗(x) for at least one value of x
where F(x) is the unknown distribution function common to the Xis and F∗(x) is given by above equation.
The Kolmogorov test for goodness of fit is used. The critical region of size α= 0.05 corresponds to values of T greater than the 0.95 quantile 0.409, obtained from Table for n=10.
The value of T is obtained by graphing the empirical distribution function S(x) on the top of the hypothesized distribution function F∗(x),as shown in Figure 2.The largest vertical distance separating the two graphs in Figure 2 is 0.290, which occurs at x = 0.710 because S(0.710) = 1.000 and F∗(0.710) = 0.710. In other words
Since T=0.290 is less than 0.409, the null hypothesis is accepted. The p-value is seen, from Table, to be larger than 0.20.

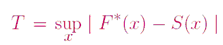



No comments:
Post a Comment