Definitions
The Dirac delta function can be loosely thought of as a function on the real line which is zero everywhere except at the origin, where it is infinite,
and which is also constrained to satisfy the identity
This heuristic definition should not be taken too seriously though. Firstly, the Dirac delta is not a function, as no function has the above properties. Moreover there exist descriptions which differ from the above conceptualizati , yet this function does not approach zero for values of x outside the origin.
, yet this function does not approach zero for values of x outside the origin.
The defining characteristic
where f is a suitable test function, cannot be achieved by any function, but the Dirac delta function can be rigorously defined either as a distribution or as a measure.
In terms of dimensional analysis, this definition of δ(x) implies that δ(x) has dimensions reciprocal to those of dx.
Fourier transform
Using Fourier transforms, one has
and therefore:
which is a statement of the orthogonality property for the Fourier kernel.
Representations of the delta function
The delta function can be viewed as the limit of a sequence of functions
where δa(x) is sometimes called a nascent delta function. This limit is in the sense that
for all continuous f.
The term approximate identity has a particular meaning in harmonic analysis, in relation to a limiting sequence to an identity element for the convolution operation (also on groups more general than the real numbers, e.g. the unit circle). There the condition is made that the limiting sequence should be of positive functions.
Some nascent delta functions are:
-
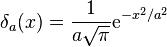
Limit of a Normal distribution 
Limit of a Cauchy distribution 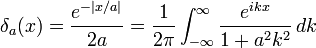
Cauchy  (see note below)
(see note below)
Limit of a rectangular function 
rectangular function  (see note below)
(see note below)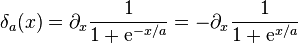
Derivative of the sigmoid (or Fermi-Dirac) function 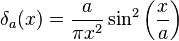

Limit of the Airy function 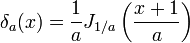
Limit of a Bessel function
Note: If δ(a, x) is a nascent delta function which is a probability distribution over the whole real line (i.e. is always non-negative between -∞ and +∞) then another nascent delta function δφ(a, x) can be built from its characteristic function as follows:
where
is the characteristic function of the nascent delta function δ(a, x). This result is related to the localization property of the continuous Fourier transform.
Probability density function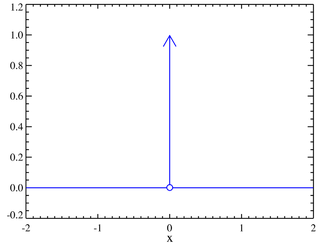 Schematic representation of the Dirac delta function for x0 = 0. A line surmounted by an arrow is usually used to schematically represent the Dirac delta function. The height of the arrow is usually used to specify the value of any multiplicative constant, which will give the area under the function. The other convention is to write the area next to the arrowhead. | |
Cumulative distribution function Using the half-maximum convention, with x0 = 0 | |
| Parameters | 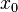 location (real) location (real) |
|---|---|
| Support | ![x \in [x_0; x_0]](http://upload.wikimedia.org/math/6/9/7/69785cd8ce1edae854a9a153c190e279.png) |
| Probability density function (pdf) | 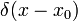 |
| Cumulative distribution function (cdf) | 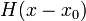 (Heaviside) (Heaviside) |
| Mean | 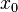 |
| Median | 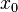 |
| Mode | 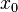 |
| Variance |  |
| Skewness |  |
| Excess kurtosis | (undefined) |
| Entropy |  |
| Moment-generati |  |
| Characteristic function |  |



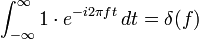
![\int_{-\infty}^\infty e^{i 2\pi f_1 t} \left[e^{i 2\pi f_2 t}\right]^*\,dt = \int_{-\infty}^\infty e^{-i 2\pi (f_2 - f_1) t} \,dt = \delta(f_2 - f_1)](http://upload.wikimedia.org/math/c/8/5/c859481b7ce6e8da26d43b953cc68812.png)
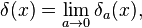


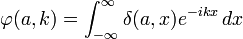
No comments:
Post a Comment