KOLMOGOROV SMIRNOV Test (TWO SAMPLE) II

Purpose:

Perform a Kolmogorov-Smirnov two sample test that two data samples come from the same distribution. Note that we are not specifying what that common distribution is.

Description: The one sample Kolmogorov-Smirnov (K-S) test is based on the empirical distribution function (ECDF). Given N data points Y₁ Y₂ ..., Y_N the ECDF is defined as

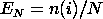
where n(i) is the number of points less than Y_i This is a step function that increases by 1/N at the value of each data point. We can graph a plot of the empirical distribution function with a cumulative distribution function for a given distribution. The one sample K-S test is based on the maximum distance between these two curves. That is,

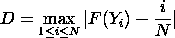
where F is the theoretical cumulative distribution function.

The two sample K-S test is a variation of this. However, instead of comparing an empirical distribution function to a theoretical distribution function, we compare the two empirical distribution functions. That is,

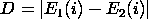
where E₁ and E₂ are the empirical distribution functions for the two samples. Note that we compute E₁ and E₂ at each point in both samples (that is both E₁ and E₂ are computed at each point in each sample).

More formally, the Kolmogorov-Smirnov two sample test statistic can be defined as follows.

H0:	The two samples come from a common distribution.
Ha:	The two samples do not come from a common distribution.
Test Statistic:	The Kolmogorov-Smir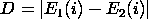nov two sample test statistic is defined as where E1 and E2 are the empirical distribution functions for the two samples.
Significance Level: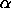
Critical Region:	The hypothesis regarding the distributional form is rejected if the test statistic, D, is greater than the critical value obtained from a table. There are several variations of these tables in the literature that use somewhat different scalings for the K-S test statistic and critical regions. These alternative formulations should be equivalent, but it is necessary to ensure that the test statistic is calculated in a way that is consistent with how the critical values were tabulated.