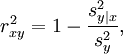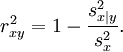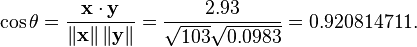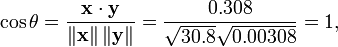In probability theory and statistics, correlation, also called correlation coefficient, indicates the strength and direction of a linear relationship between two random variables. In general statistical usage, correlation or co-relation refers to the departure of two variables from independence. In this broad sense there are several coefficients, measuring the degree of correlation, adapted to the nature of data.
A number of different coefficients are used for different situations. The best known is the Pearson product-moment correlation coefficient, which is obtained by dividing the covariance of the two variables by the product of their standard deviations. Despite its name, it was first introduced by Francis Galton.
Pearson's product-moment coefficient
-
Mathematical properties
The correlation coefficient ρX, Y between two random variables X and Y with expected values μX and μY and standard deviations σX and σY is defined as:
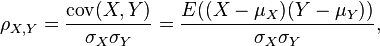
where E is the expected value operator and cov means covariance. Since μX = E(X), σX2 = E(X2) − E2(X) and likewise for Y, we may also write

The correlation is defined only if both of the standard deviations are finite and both of them are nonzero. It is a corollary of the Cauchy-Schwarz inequality that the correlation cannot exceed 1 in absolute value.
The correlation is 1 in the case of an increasing linear relationship, −1 in the case of a decreasing linear relationship, and some value in between in all other cases, indicating the degree of linear dependence between the variables. The closer the coefficient is to either −1 or 1, the stronger the correlation between the variables.
If the variables are independent then the correlation is 0, but the converse is not true because the correlation coefficient detects only linear dependencies between two variables. Here is an example: Suppose the random variable X is uniformly distributed on the interval from −1 to 1, and Y = X2. Then Y is completely determined by X, so that X and Y are dependent, but their correlation is zero; they are uncorrelated. However, in the special case when X and Y are jointly normal, independence is equivalent to uncorrelatedness.
A correlation between two variables is diluted in the presence of measurement error around estimates of one or both variables, in which case disattenuation provides a more accurate coefficient .

Positive linear correlations between 1000 pairs of numbers. The data are graphed on the lower left and their correlation coefficients listed on the upper right. Each square in the upper right corresponds to its mirror-image square in the lower left, the "mirror" being the diagonal of the whole array. Each set of points correlates maximally with itself, as shown on the diagonal (all correlations = +1).
The sample correlation
If we have a series of n measurements of X and Y written as xi and yi where i = 1, 2, ..., n, then the Pearson product-moment correlation coefficient can be used to estimate the correlation of X and Y . The Pearson coefficient is also known as the "sample correlation coefficient". It is especially important if X and Y are both normally distributed. The Pearson correlation coefficient is then the best estimate of the correlation of X and Y . The Pearson correlation coefficient is written:

where 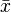 and
and  are the sample means of X and Y , sx and sy are the sample standard deviations of X and Y and the sum is from i = 1 to n. As with the population correlation, we may rewrite this as
are the sample means of X and Y , sx and sy are the sample standard deviations of X and Y and the sum is from i = 1 to n. As with the population correlation, we may rewrite this as

Again, as is true with the population correlation, the absolute value of the sample correlation must be less than or equal to 1. Though the above formula conveniently suggests a single-pass algorithm for calculating sample correlations, it is notorious for its numerical instability (see below for something more accurate).
The square of the sample correlation coefficient, which is also known as the coefficient of determination, is the fraction of the variance in yi that is accounted for by a linear fit of xi to yi . This is written
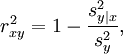
where sy|x2 is the square of the error of a linear regression of xi on yi by the equation y = a + bx:

and sy2 is just the variance of y:

Note that since the sample correlation coefficient is symmetric in xi and yi , we will get the same value for a fit of xi to yi :
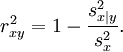
This equation also gives an intuitive idea of the correlation coefficient for higher dimensions. Just as the above described sample correlation coefficient is the fraction of variance accounted for by the fit of a 1-dimensional linear submanifold to a set of 2-dimensional vectors (xi , yi ), so we can define a correlation coefficient for a fit of an m-dimensional linear submanifold to a set of n-dimensional vectors. For example, if we fit a plane z = a + bx + cy to a set of data (xi , yi , zi ) then the correlation coefficient of z to x and y is

Geometric Interpretation of correlation
The correlation coefficient can also be viewed as the cosine of the angle between the two vectors of samples drawn from the two random variables.
Caution: This method only works with centered data, i.e., data which have been shifted by the sample mean so as to have an average of zero. Some practitioners prefer an uncentered (non-Pearson-compliant) correlation coefficient. See the example below for a comparison.
As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3, 5, 8) and y = (0.11, 0.12, 0.13, 0.15, 0.18).
By the usual procedure for finding the angle between two vectors (see dot product), the uncentered correlation coefficient is:
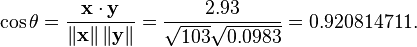
Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x. The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by E(x) = 3.8 and y by E(y) = 0.138) yields x = (-2.8, -1.8, -0.8, 1.2, 4.2) and y = (-0.028, -0.018, -0.008, 0.012, 0.042), from which
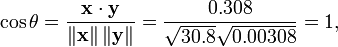
as expected.
Interpretation of the size of a correlation
| Correlation | Negative | Positive |
| Small | −0.29 to −0.10 | 0.10 to 0.29 |
| Medium | −0.49 to −0.30 | 0.30 to 0.49 |
| Large | −1.00 to −0.50 | 0.50 to 1.00 |
Several authors have offered guidelines for the interpretation of a correlation coefficient. Cohen (1988),[1] for example, has suggested the following interpretations for correlations in psychological research, in the table on the right.
As Cohen himself has observed, however, all such criteria are in some ways arbitrary and should not be observed too strictly. This is because the interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.9 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences where there may be a greater contribution from complicating factors.
Non-parametric correlation coefficients
Pearson's correlation coefficient is a parametric statistic, and it may be less useful if the underlying assumption of normality is violated. Non-parametric correlation methods, such as Chi-square, Point biserial correlation, Spearman's ρ and Kendall's τ may be useful when distributions are not normal; they are a little less powerful than parametric methods if the assumptions underlying the latter are met, but are less likely to give distorted results when the assumptions fail.
Other measures of dependence among random variables
To get a measure for more general dependencies in the data (also nonlinear) it is better to use the correlation ratio which is able to detect almost any functional dependency, or mutual information/total correlation which is capable of detecting even more general dependencies.
Copulas and correlation
The information given by a correlation coefficient is not enough to define the dependence structure between random variables; to fully capture it we must consider a copula between them. The correlation coefficient completely defines the dependence structure only in very particular cases, for example when the cumulative distribution functions are the multivariate normal distributions. In the case of elliptic distributions it characterizes the (hyper-)ellipses of equal density, however, it does not completely characterize the dependence structure (for example, the a multivariate t-distribution's degrees of freedom determine the level of tail dependence).
Correlation matrices
The correlation matrix of n random variables X1, ..., Xn is the n × n matrix whose i,j entry is corr(Xi, Xj). If the measures of correlation used are product-moment coefficients, the correlation matrix is the same as the covariance matrix of the standardized random variables Xi /SD(Xi) for i = 1, ..., n. Consequently it is necessarily a positive-semidefinite matrix.
The correlation matrix is symmetric because the correlation between Xi and Xj is the same as the correlation between Xj and Xi.
Removing correlation
It is always possible to remove the correlation between zero-mean random variables with a linear transform, even if the relationship between the variables is nonlinear. Suppose a vector of n random variables is sampled m times. Let X be a matrix where Xi,j is the jth variable of sample i. Let Zr,c be an r by c matrix with every element 1. Then D is the data transformed so every random variable has zero mean, and T is the data transformed so all variables have zero mean, unit variance, and zero correlation with all other variables.


where an exponent of -1/2 represents the matrix square root of the inverse of a matrix. The covariance matrix of T will be the identity matrix. If a new data sample x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:


Common misconceptions about correlation
Correlation and causality
The conventional dictum that "correlation does not imply causation" means that correlation cannot be validly used to infer a causal relationship between the variables. This dictum should not be taken to mean that correlations cannot indicate causal relations. However, the causes underlying the correlation, if any, may be indirect and unknown. Consequently, establishing a correlation between two variables is a not sufficient condition to establish a causal relationship (in either direction).
Here is a simple example: hot weather may cause both crime and ice-cream purchases. Therefore crime is correlated with ice-cream purchases. But crime does not cause ice-cream purchases and ice-cream purchases do not cause crime.
A correlation between age and height in children is fairly causally transparent, but a correlation between mood and health in people is less so. Does improved mood lead to improved health? Or does good health lead to good mood? Or does some other factor underlie both? Or is it pure coincidence? In other words, a correlation can be taken as evidence for a possible causal relationship, but cannot indicate what the causal relationship, if any, might be.
Correlation and linearity

Four sets of data with the same correlation of 0.81
While Pearson correlation indicates the strength of a linear relationship between two variables, its value alone may not be sufficient to evaluate this relationship, especially in the case where the assumption of normality is incorrect.
The image on the right shows scatterplots of Anscombe's quartet, a set of four different pairs of variables created by Francis Anscombe.[2] The four y variables have the same mean (7.5), standard deviation (4.12), correlation (0.81) and regression line (y = 3 + 0.5x). However, as can be seen on the plots, the distribution of the variables is very different. The first one (top left) seems to be distributed normally, and corresponds to what one would expect when considering two variables correlated and following the assumption of normality. The second one (top right) is not distributed normally; while an obvious relationship between the two variables can be observed, it is not linear, and the Pearson correlation coefficient is not relevant. In the third case (bottom left), the linear relationship is perfect, except for one outlier which exerts enough influence to lower the correlation coefficient from 1 to 0.81. Finally, the fourth example (bottom right) shows another example when one outlier is enough to produce a high correlation coefficient, even though the relationship between the two variables is not linear.
These examples indicate that the correlation coefficient, as a summary statistic, cannot replace the individual examination of the data.
Computing correlation accurately in a single pass
The following algorithm (in pseudocode) will estimate correlation with good numerical stability
sum_sq_x = 0
sum_sq_y = 0
sum_coproduct = 0
mean_x = x[1]
mean_y = y[1]
for i in 2 to N:
sweep = (i - 1.0) / i
delta_x = x[i] - mean_x
delta_y = y[i] - mean_y
sum_sq_x += delta_x * delta_x * sweep
sum_sq_y += delta_y * delta_y * sweep
sum_coproduct += delta_x * delta_y * sweep
mean_x += delta_x / i
mean_y += delta_y / i
pop_sd_x = sqrt( sum_sq_x / N )
pop_sd_y = sqrt( sum_sq_y / N )
cov_x_y = sum_coproduct / N
correlation = cov_x_y / (pop_sd_x * pop_sd_y)
For an enlightening experiment, check the correlation of {900,000,000 + i for i=1...100} with {900,000,000 - i for i=1...100}, perhaps with a few values modified. Poor algorithms will fail.
Currency correlation
Currency correlation is correlation between two currency pairs, or more generally, correlations between values of commodities, stocks and bonds markets. It is used as a tool to predict changes in market value.
 Say we have a set of data,
Say we have a set of data,  , shown at the left. If we have reason to believe that there exists a linear relationship between the variables x and y, we can plot the data and draw a "best-fit" straight line through the data. Of course, this relationship is governed by the familiar equation
, shown at the left. If we have reason to believe that there exists a linear relationship between the variables x and y, we can plot the data and draw a "best-fit" straight line through the data. Of course, this relationship is governed by the familiar equation  . We can then find the slope, m, and y-intercept, b, for the data, which are shown in the figure below.
. We can then find the slope, m, and y-intercept, b, for the data, which are shown in the figure below. 


 . Instead, we can apply a statistical treatment known as linear regression to the data and determine these constants.
. Instead, we can apply a statistical treatment known as linear regression to the data and determine these constants.  with n data points, the slope, y-intercept and correlation coefficient, r, can be determined using the following:
with n data points, the slope, y-intercept and correlation coefficient, r, can be determined using the following: 










 . The value of n is 10. So these values can now be substituted back into the equation,
. The value of n is 10. So these values can now be substituted back into the equation,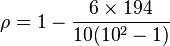
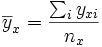 and
and 

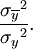
 and values of
and values of  is linear (which is certainly true when there are only two possibilities for x) this will give the same result as the square of the
is linear (which is certainly true when there are only two possibilities for x) this will give the same result as the square of the 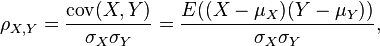



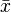 and
and  are the sample
are the sample