The Fourier series is a mathematical tool used for analyzing periodic functions by decomposing such a function into a weighted sum of much simpler sinusoidal component functions sometimes referred to as normal Fourier modes, or simply modes for short. The weights, or coefficients, of the modes, are a one-to-one mapping of the original function. Generalizations
include generalized Fourier series and other expansions over orthonormal bases.
Definition
Given a complex-valued function f of real argument t, f: R → C, where f(t) is piecewise smooth and continuous, periodic with period T, and square-integrab
where
-
- T = t2 − t1 is the period,
- t1 and t2 are integration bounds.
The Fourier series expansion of f is
where, for any non-negative integer n,
Equivalently, in complex exponential form,
where:
-

- i is the imaginary unit, and
 in accordance with Euler's formula.
in accordance with Euler's formula.
For a formal justification, see Modern derivation of the Fourier coefficients below.
Canonical form
In the special case where the period T = 2π, we have
In this case, the Fourier series expansion reduces to a particularly simple form:
where
for any non-negative integer n.
or, equivalently:
where
Choice of the form
The form for period T can be easily derived from the canonical one with the change of variable defined by  . Therefore, both formulations are equivalent. However, the form for period T is used in most practical cases because it is directly applicable. For the theory, the canonical form is preferred because it is more elegant and easier to interpret mathematically,
. Therefore, both formulations are equivalent. However, the form for period T is used in most practical cases because it is directly applicable. For the theory, the canonical form is preferred because it is more elegant and easier to interpret mathematically,
Examples
Simple Fourier series
Let f be periodic of period 2π, with f(x) = x for x from −π to π. Note that this function is a periodic version of the identity function.
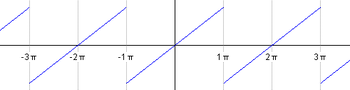
We will compute the Fourier coefficients for this function.
Notice that an are 0 because the  are even functions. Hence the Fourier series for this function is:
are even functions. Hence the Fourier series for this function is:
One application of this Fourier series is to compute the value of the Riemann zeta function at s = 2; by Parseval's theorem, we have:
0}\left[2\frac{(-1)^n}{n}\right]^2" src="http://upload.wikimedia.org/math/e/7/7/e777681f5b32083c015c6ba54578e77f.png">
which yields: 0}\frac{1}{n^2}=\frac{\pi^2}{6}" src="http://upload.wikimedia.org/math/3/5/9/359981037d4391ebe85b915baae0b473.png">.

![f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}[a_n \cos(\omega_n t) + b_n \sin(\omega_n t)]](http://upload.wikimedia.org/math/a/2/6/a26170eaeb5b0766650ba8bab7d03081.png)
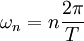 is the nth
is the nth  are the
are the  are the
are the 
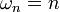
![f(t) = \frac{1}{2} a_0 +\sum_{n=1}^{\infty}[a_n \cos(nt) + b_n \sin(nt)]](http://upload.wikimedia.org/math/9/c/9/9c9c806bb0d5794abf870672b90e9eeb.png)

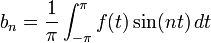



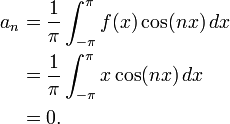
![\begin{align} b_n &{}= \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)\,dx \\ &{}= \frac{1}{\pi}\int_{-\pi}^{\pi} x \sin(nx)\, dx \\ &{}= \frac{2}{\pi}\int_{0}^{\pi} x\sin(nx)\, dx \\ &{}= \frac{2}{\pi} \left(\left[-\frac{x\cos(nx)}{n}\right]_0^{\pi} + \left[\frac{\sin(nx)}{n^2}\right]_0^{\pi}\right) \\ &{}= 2\frac{(-1)^{n+1}}{n}.\end{align}](http://upload.wikimedia.org/math/9/6/4/96499a0d78c630eed6f3e0fb56916cf9.png)
![f(x)=\frac{a_0}{2} + \sum_{n=1}^{\infty}\left[a_n\cos\left(nx\right)+b_n\sin\left(nx\right)\right]](http://upload.wikimedia.org/math/5/9/8/59898330aa663ec50aa3967e17b4298e.png)
![=2\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n} \sin(nx), \quad \forall x\in [-\pi,\pi].](http://upload.wikimedia.org/math/1/a/4/1a4076e2dce0314db149126b84b2c36f.png)
No comments:
Post a Comment