M2P2 Algebra
Lecturer: Prof M W Liebeck
Recommended books
R.. Allenby, Rings, Fields and Groups, Arnold
I.N. Herstein, Topics in Algebra
For linear algebra, here are a few good ones:
J. Fraleigh and R. Beauregard, Linear Algebra, Addison Wesley
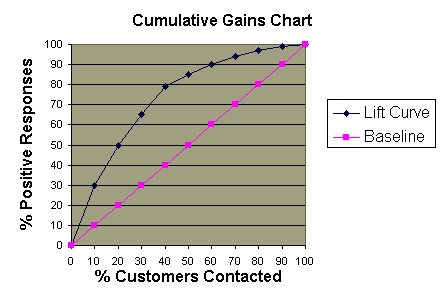
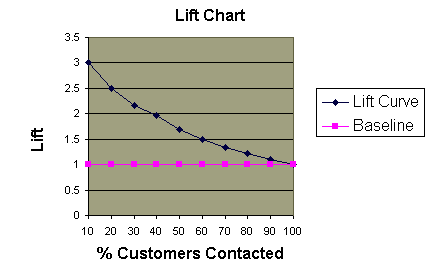


 The sensitivity and specificity of a diagnostic test depends on more than just the "quality" of the test--they also depend on the definition of what constitutes an abnormal test. Look at the the idealized graph at right showing the number of patients with and without a disease arranged according to the value of a diagnostic test. This distributions overlap--the test (like most) does not distinguish normal from disease with 100% accuracy. The area of overlap indicates where the test cannot distinguish normal from disease. In practice, we choose a cutpoint (indicated by the vertical black line) above which we consider the test to be abnormal and below which we consider the test to be normal. The position of the cutpoint will determine the number of true positive, true negatives, false positives and false negatives. We may wish to use different cutpoints for different clinical situations if we wish to minimize one of the erroneous types of test results.
The sensitivity and specificity of a diagnostic test depends on more than just the "quality" of the test--they also depend on the definition of what constitutes an abnormal test. Look at the the idealized graph at right showing the number of patients with and without a disease arranged according to the value of a diagnostic test. This distributions overlap--the test (like most) does not distinguish normal from disease with 100% accuracy. The area of overlap indicates where the test cannot distinguish normal from disease. In practice, we choose a cutpoint (indicated by the vertical black line) above which we consider the test to be abnormal and below which we consider the test to be normal. The position of the cutpoint will determine the number of true positive, true negatives, false positives and false negatives. We may wish to use different cutpoints for different clinical situations if we wish to minimize one of the erroneous types of test results.

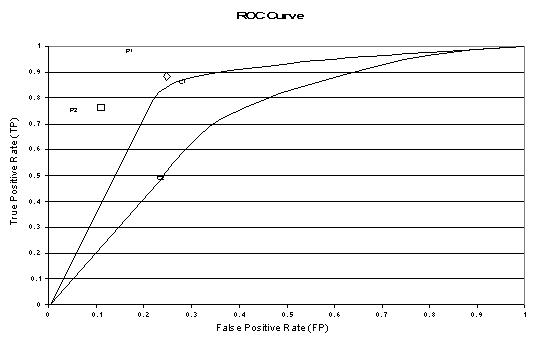
 The graph at right shows three ROC curves representing excellent, good, and worthless tests plotted on the same graph. The accuracy of the test depends on how well the test separates the group being tested into those with and without the disease in question. Accuracy is measured by the area under the ROC curve. An area of 1 represents a perfect test; an area of .5 represents a worthless test. A rough guide for classifying the accuracy of a diagnostic test is the traditional academic point system:
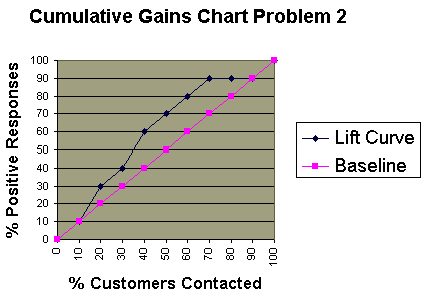
The graph at right shows three ROC curves representing excellent, good, and worthless tests plotted on the same graph. The accuracy of the test depends on how well the test separates the group being tested into those with and without the disease in question. Accuracy is measured by the area under the ROC curve. An area of 1 represents a perfect test; an area of .5 represents a worthless test. A rough guide for classifying the accuracy of a diagnostic test is the traditional academic point system:  ROC curves can also be constructed from clinical prediction rules. The graphs at right come from a study of how clinical findings predict strep throat (Wigton RS, Connor JL, Centor RM. Transportability of a decision rule for the diagnosis of streptococcal pharyngitis. Arch Intern Med. 1986;146:81-83.) In that study, the presence of tonsillar exudate, fever, adenopathy and the absence of cough all predicted strep. The curves were constructed by computing the sensitivity and specificity of increasing numbers of clinical findings (from 0 to 4) in predicting strep. The study compared patients in Virginia and Nebraska and found that the rule performed more accurately in Virginia (area under the curve = .78) compared to Nebraska (area under the curve = .73). These differences turn out not to be statistically different, however.
ROC curves can also be constructed from clinical prediction rules. The graphs at right come from a study of how clinical findings predict strep throat (Wigton RS, Connor JL, Centor RM. Transportability of a decision rule for the diagnosis of streptococcal pharyngitis. Arch Intern Med. 1986;146:81-83.) In that study, the presence of tonsillar exudate, fever, adenopathy and the absence of cough all predicted strep. The curves were constructed by computing the sensitivity and specificity of increasing numbers of clinical findings (from 0 to 4) in predicting strep. The study compared patients in Virginia and Nebraska and found that the rule performed more accurately in Virginia (area under the curve = .78) compared to Nebraska (area under the curve = .73). These differences turn out not to be statistically different, however. 


 .
.








