Overview of Statistical Test [***recommended***]

Choosing a statistical test This is chapter 37 of Intuitive Biostatistics (ISBN 0-19-508607-4) by Harvey Motulsky. Copyright © 1995 by Oxford University Press Inc. All rights reserved. You may order the book from GraphPad Software with a software purchase, from any academic bookstore, or from amazon.com. Learn how to interpret the results of statistical tests and about our programs GraphPad InStat and GraphPad Prism.

REVIEW OF AVAILABLE STATISTICAL TESTS This book has discussed many different statistical tests. To select the right test, ask yourself two questions: What kind of data have you collected? What is your goal? Then refer to Table 37.1. All tests are described in this book and are performed by InStat, except for tests marked with asterisks. Tests labeled with a single asterisk are briefly mentioned in this book, and tests labeled with two asterisks are not mentioned at all. Table 37.1. Selecting a statistical test Type of Data Goal Measurement (from Gaussian Population) Rank, Score, or Measurement (from Non- Gaussian Population) Binomial (Two Possible Outcomes) Survival Time Describe one group Mean, SD Median, interquartile range Proportion Kaplan Meier survival curve Compare one group to a hypothetical value One-sample t test Wilcoxon test Chi-square or Binomial test ** Compare two unpaired groups Unpaired t test Mann-Whitney test Fisher's test (chi-square for large samples) Log-rank test or Mantel-Haenszel* Compare two paired groups Paired t test Wilcoxon test McNemar's test Conditional proportional hazards regression* Compare three or more unmatched groups One-way ANOVA Kruskal-Wallis test Chi-square test Cox proportional hazard regression** Compare three or more matched groups Repeated-measures ANOVA Friedman test Cochrane Q** Conditional proportional hazards regression** Quantify association between two variables Pearson correlation Spearman correlation Contingency coefficients** Predict value from another measured variable Simple linear regression or Nonlinear regression Nonparametric regression** Simple logistic regression* Cox proportional hazard regression* Predict value from several measured or binomial variables Multiple linear regression* or Multiple nonlinear regression** Multiple logistic regression* Cox proportional hazard regression* REVIEW OF NONPARAMETRIC TESTS Choosing the right test to compare measurements is a bit tricky, as you must choose between two families of tests: parametric and nonparametric. Many -statistical test are based upon the assumption that the data are sampled from a Gaussian distribution. These tests are referred to as parametric tests. Commonly used parametric tests are listed in the first column of the table and include the t test and analysis of variance. Tests that do not make assumptions about the population distribution are referred to as nonparametric- tests. You've already learned a bit about nonparametric tests in previous chapters. All commonly used nonparametric tests rank the outcome variable from low to high and then analyze the ranks. These tests are listed in the second column of the table and include the Wilcoxon, Mann-Whitney test, and Kruskal-Wallis tests. These tests are also called distribution-free tests. CHOOSING BETWEEN PARAMETRIC AND NONPARAMETRIC TESTS: THE EASY CASES Choosing between parametric and nonparametric tests is sometimes easy. You should definitely choose a parametric test if you are sure that your data are sampled from a population that follows a Gaussian distribution (at least approximately). You should definitely select a nonparametric test in three situations: • The outcome is a rank or a score and the population is clearly not Gaussian. Examples include class ranking of students, the Apgar score for the health of newborn babies (measured on a scale of 0 to IO and where all scores are integers), the visual analogue score for pain (measured on a continuous scale where 0 is no pain and 10 is unbearable pain), and the star scale commonly used by movie and restaurant critics (* is OK, ***** is fantastic). • Some values are "off the scale," that is, too high or too low to measure. Even if the population is Gaussian, it is impossible to analyze such data with a parametric test since you don't know all of the values. Using a nonparametric test with these data is simple. Assign values too low to measure an arbitrary very low value and assign values too high to measure an arbitrary very high value. Then perform a nonparametric test. Since the nonparametric test only knows about the relative ranks of the values, it won't matter that you didn't know all the values exactly. • The data ire measurements, and you are sure that the population is not distributed in a Gaussian manner. If the data are not sampled from a Gaussian distribution, consider whether you can transformed the values to make the distribution become Gaussian. For example, you might take the logarithm or reciprocal of all values. There are often biological or chemical reasons (as well as statistical ones) for performing a particular transform. CHOOSING BETWEEN PARAMETRIC AND NONPARAMETRIC TESTS: THE HARD CASES It is not always easy to decide whether a sample comes from a Gaussian population. Consider these points: • If you collect many data points (over a hundred or so), you can look at the distribution of data and it will be fairly obvious whether the distribution is approximately bell shaped. A formal statistical test (Kolmogorov-Smirnoff test, not explained in this book) can be used to test whether the distribution of the data differs significantly from a Gaussian distribution. With few data points, it is difficult to tell whether the data are Gaussian by inspection, and the formal test has little power to discriminate between Gaussian and non-Gaussian distributions. • You should look at previous data as well. Remember, what matters is the distribution of the overall population, not the distribution of your sample. In deciding whether a population is Gaussian, look at all available data, not just data in the current experiment. • Consider the source of scatter. When the scatter comes from the sum of numerous sources (with no one source contributing most of the scatter), you expect to find a roughly Gaussian distribution. When in doubt, some people choose a parametric test (because they aren't sure the Gaussian assumption is violated), and others choose a nonparametric test (because they aren't sure the Gaussian assumption is met). CHOOSING BETWEEN PARAMETRIC AND NONPARAMETRIC TESTS: DOES IT MATTER? Does it matter whether you choose a parametric or nonparametric test? The answer depends on sample size. There are four cases to think about: • Large sample. What happens when you use a parametric test with data from a nongaussian population? The central limit theorem (discussed in Chapter 5) ensures that parametric tests work well with large samples even if the population is non-Gaussian. In other words, parametric tests are robust to deviations from Gaussian distributions, so long as the samples are large. The snag is that it is impossible to say how large is large enough, as it depends on the nature of the particular non-Gaussian distribution. Unless the population distribution is really weird, you are probably safe choosing a parametric test when there are at least two dozen data points in each group. • Large sample. What happens when you use a nonparametric test with data from a Gaussian population? Nonparametric tests work well with large samples from Gaussian populations. The P values tend to be a bit too large, but the discrepancy is small. In other words, nonparametric tests are only slightly less powerful than parametric tests with large samples. • Small samples. What happens when you use a parametric test with data from nongaussian populations? You can't rely on the central limit theorem, so the P value may be inaccurate. • Small samples. When you use a nonparametric test with data from a Gaussian population, the P values tend to be too high. The nonparametric tests lack statistical power with small samples. Thus, large data sets present no problems. It is usually easy to tell if the data come from a Gaussian population, but it doesn't really matter because the nonparametric tests are so powerful and the parametric tests are so robust. Small data sets present a dilemma. It is difficult to tell if the data come from a Gaussian population, but it matters a lot. The nonparametric tests are not powerful and the parametric tests are not robust. ONE- OR TWO-SIDED P VALUE? With many tests, you must choose whether you wish to calculate a one- or two-sided P value (same as one- or two-tailed P value). The difference between one- and two-sided P values was discussed in Chapter 10. Let's review the difference in the context of a t test. The P value is calculated for the null hypothesis that the two population means are equal, and any discrepancy between the two sample means is due to chance. If this null hypothesis is true, the one-sided P value is the probability that two sample means would differ as much as was observed (or further) in the direction specified by the hypothesis just by chance, even though the means of the overall populations are actually equal. The two-sided P value also includes the probability that the sample means would differ that much in the opposite direction (i.e., the other group has the larger mean). The two-sided P value is twice the one-sided P value. A one-sided P value is appropriate when you can state with certainty (and before collecting any data) that there either will be no difference between the means or that the difference will go in a direction you can specify in advance (i.e., you have specified which group will have the larger mean). If you cannot specify the direction of any difference before collecting data, then a two-sided P value is more appropriate. If in doubt, select a two-sided P value. If you select a one-sided test, you should do so before collecting any data and you need to state the direction of your experimental hypothesis. If the data go the other way, you must be willing to attribute that difference (or association or correlation) to chance, no matter how striking the data. If you would be intrigued, even a little, by data that goes in the "wrong" direction, then you should use a two-sided P value. For reasons discussed in Chapter 10, I recommend that you always calculate a two-sided P value. PAIRED OR UNPAIRED TEST? When comparing two groups, you need to decide whether to use a paired test. When comparing three or more groups, the term paired is not apt and the term repeated measures is used instead. Use an unpaired test to compare groups when the individual values are not paired or matched with one another. Select a paired or repeated-measures test when values represent repeated measurements on one subject (before and after an intervention) or measurements on matched subjects. The paired or repeated-measures tests are also appropriate for repeated laboratory experiments run at different times, each with its own control. You should select a paired test when values in one group are more closely correlated with a specific value in the other group than with random values in the other group. It is only appropriate to select a paired test when the subjects were matched or paired before the data were collected. You cannot base the pairing on the data you are analyzing. FISHER'S TEST OR THE CHI-SQUARE TEST? When analyzing contingency tables with two rows and two columns, you can use either Fisher's exact test or the chi-square test. The Fisher's test is the best choice as it always gives the exact P value. The chi-square test is simpler to calculate but yields only an approximate P value. If a computer is doing the calculations, you should choose Fisher's test unless you prefer the familiarity of the chi-square test. You should definitely avoid the chi-square test when the numbers in the contingency table are very small (any number less than about six). When the numbers are larger, the P values reported by the chi-square and Fisher's test will he very similar. The chi-square test calculates approximate P values, and the Yates' continuity correction is designed to make the approximation better. Without the Yates' correction, the P values are too low. However, the correction goes too far, and the resulting P value is too high. Statisticians give different recommendations regarding Yates' correction. With large sample sizes, the Yates' correction makes little difference. If you select Fisher's test, the P value is exact and Yates' correction is not needed and is not available. REGRESSION OR CORRELATION? Linear regression and correlation are similar and easily confused. In some situations it makes sense to perform both calculations. Calculate linear correlation if you measured both X and Y in each subject and wish to quantity how well they are associated. Select the Pearson (parametric) correlation coefficient if you can assume that both X and Y are sampled from Gaussian populations. Otherwise choose the Spearman nonparametric correlation coefficient. Don't calculate the correlation coefficient (or its confidence interval) if you manipulated the X variable. Calculate linear regressions only if one of the variables (X) is likely to precede or cause the other variable (Y). Definitely choose linear regression if you manipulated the X variable. It makes a big difference which variable is called X and which is called Y, as linear regression calculations are not symmetrical with respect to X and Y. If you swap the two variables, you will obtain a different regression line. In contrast, linear correlation calculations are symmetrical with respect to X and Y. If you swap the labels X and Y, you will still get the same correlation coefficient.

Statistical Data Analysis: Elementary Concepts

Understanding Statistical Inference

Statistical inference is based upon mathematical laws of probability. The following example will give you the basic ideas.

Statistical Inference & The Coin Toss

Suppose we want to do a few coin tosses (sample) so that we can decide if a particular coin is equally likely to land head or tail over an infinite number of tosses (population).

If we toss the coin ten times and get 6 heads and 4 tails, we might suspect the coin is biased towards heads, but we wouldn't be very confident about this, because it's not that unusual (not that improbable) to get 6 heads out of 10.

On the other hand, if we toss the coin ten times and get 10 heads - we would be more confident that the coin is biased towards heads, because it is very unusual (not very probable at all) that we would get this result from an unbiased coin.

Statistical Data Analysis: Hypothesis Testing

The most common kind of statistical inference is hypothesis testing. Statistical data analysis allows us to use mathematical principles to decide how likely it is that our sample results match our hypothesis about a population. For example, if our research hypothesis is that the coin is not fair, but is actually biased towards heads - we can use principles of statistics to tell us how likely it is that we could get our sample results even if the coin were fair after all (null hypothesis).

If the probability of getting our sample results from a fair coin is very low, we feel confident in rejecting the null hypothesis (that the coin is fair). Even though we can't say for sure (because even a fair coin could produce our sample results), we can say that the results of our study support the hypothesis that the coin is indeed biased.

When we make this decision based on statistical data analysis, this is statistical inference.

Statistical Data Analysis: p-value

In statistical hypothesis testing we use a p-value (probability value) to decide whether we have enough evidence to reject the null hypothesis and say our research hypothesis is supported by the data.

The p-value is a numerical statement of how likely it is that we could have gotten our sample data (e.g., 10 heads) even if the null hypothesis is true (e.g., fair coin). By convention, if the p-value is less than 0.05 (p <>

KOLMOGOROV SMIRNOV Test (TWO SAMPLE) II

Purpose:

Perform a Kolmogorov-Smirnov two sample test that two data samples come from the same distribution. Note that we are not specifying what that common distribution is.

Description: The one sample Kolmogorov-Smirnov (K-S) test is based on the empirical distribution function (ECDF). Given N data points Y₁ Y₂ ..., Y_N the ECDF is defined as

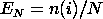
where n(i) is the number of points less than Y_i This is a step function that increases by 1/N at the value of each data point. We can graph a plot of the empirical distribution function with a cumulative distribution function for a given distribution. The one sample K-S test is based on the maximum distance between these two curves. That is,

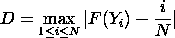
where F is the theoretical cumulative distribution function.

The two sample K-S test is a variation of this. However, instead of comparing an empirical distribution function to a theoretical distribution function, we compare the two empirical distribution functions. That is,

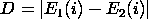
where E₁ and E₂ are the empirical distribution functions for the two samples. Note that we compute E₁ and E₂ at each point in both samples (that is both E₁ and E₂ are computed at each point in each sample).

More formally, the Kolmogorov-Smirnov two sample test statistic can be defined as follows.

H0:	The two samples come from a common distribution.
Ha:	The two samples do not come from a common distribution.
Test Statistic:	The Kolmogorov-Smir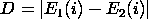nov two sample test statistic is defined as where E1 and E2 are the empirical distribution functions for the two samples.
Significance Level: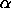
Critical Region:	The hypothesis regarding the distributional form is rejected if the test statistic, D, is greater than the critical value obtained from a table. There are several variations of these tables in the literature that use somewhat different scalings for the K-S test statistic and critical regions. These alternative formulations should be equivalent, but it is necessary to ensure that the test statistic is calculated in a way that is consistent with how the critical values were tabulated.

Nonparametric Methods II (Brief Overview)

Basically, there is at least one nonparametric equivalent for each parametric general type of test. In general, these tests fall into the following categories:

• Tests of differences between groups (independent samples);
• Tests of differences between variables (dependent samples);
• Tests of relationships between variables.

Differences between independent groups.

• Usually, when we have two samples that we want to compare concerning their mean value for some variable of interest, we would use the t-test for independent samples; nonparametric alternatives for this test are the Wald-Wolfowitz runs test, the Mann-Whitney U test, and the Kolmogorov-Smirnov two-sample test.
  
• If we have multiple groups, we would use analysis of variance see ANOVA/MANOVA; the nonparametric equivalents to this method are the Kruskal-Wallis analysis of ranks and the Median test.

Differences between dependent groups.

• If we want to compare two variables measured in the same sample we would customarily use the t-test for dependent samples ( for example, if we wanted to compare students' math skills at the beginning of the semester with their skills at the end of the semester). Nonparametric alternatives to this test are the Sign test and Wilcoxon's matched pairs test.
  
• If the variables of interest are dichotomous in nature (i.e., "pass" vs. "no pass") then McNemar's Chi-square test is appropriate.
  
• If there are more than two variables that were measured in the same sample, then we would customarily use repeated measures ANOVA. Nonparametric alternatives to this method are Friedman's two-way analysis of variance and Cochran Q test (if the variable was measured in terms of categories, e.g., "passed" vs. "failed"). Cochran Q is particularly useful for measuring changes in frequencies (proportions) across time.

Relationships between variables. To express a relationship between two variables one usually computes the correlation coefficient. Nonparametric equivalents to the standard correlation coefficient are Spearman R, Kendall Tau, and coefficient Gamma (see Nonparametric correlations).

• If the two variables of interest are categorical in nature (e.g., "passed" vs. "failed" by "male" vs. "female") appropriate nonparametric statistics for testing the relationship between the two variables are the Chi-square test, the Phi coefficient, and the Fisher exact test.
  
• In addition, a simultaneous test for relationships between multiple cases is available: Kendall coefficient of concordance. This test is often used for expressing inter-rater agreement among independent judges who are rating (ranking) the same stimuli.

Descriptive statistics. When one's data are not normally distributed, and the measurements at best contain rank order information, then computing the standard descriptive statistics (e.g., mean, standard deviation) is sometimes not the most informative way to summarize the data. For example, in the area of psychometrics it is well known that the rated intensity of a stimulus (e.g., perceived brightness of a light) is often a logarithmic function of the actual intensity of the stimulus (brightness as measured in objective units of Lux). In this example, the simple mean rating (sum of ratings divided by the number of stimuli) is not an adequate summary of the average actual intensity of the stimuli. (In this example, one would probably rather compute the geometric mean.)

• Nonparametrics and Distributions will compute a wide variety of measures of location (mean, median, mode, etc.) and dispersion (variance, average deviation, quartile range, etc.) to provide the "complete picture" of one's data.

A Partial Syllabus of Data Analysis

Probability

PROBABILITY THEORY :

Distributions

	CONTINUOUS DISTRIBUTIONS :
	DISCRETE DISTRIBUTIONS :

Linear Regression

	SIMPLE LINEAR REGRESSION
	MULTIPLE LINEAR REGRESSION

Estimation

Confidence intervals Confidence intervals for means of normal distributions One sample confidence intervals. Two samples confidence intervals : paired samples, independent samples (variances known, unknown but equal, unknown and not equal). Approximate confidence intervals on means Asymptotic interval (no demonstration). Welch's approximation. Mean Square Error (MSE) Mean Square Error (MSE) Minimum Mean Square Error (MMSE) estimators MSE of a parameter estimator. Best estimate of a random variable X. Best estimate of X when a second r.v. Y is available. Properties of Minimum Mean Square Error estimators. Sufficient statistic First examples of sufficient statistics Sufficient statistics for : * The Bernoulli distribution b(p), * The uniform distribution U[0, q], * The Poisson distribution P(l), from the definition only. The factorization theorem and applications A necessary and sufficient condition for a statistic to be sufficient. Examples : Bernoulli, uniform, Poisson, normal (two methods), Gamma, exponential.

Tests

ANOVA (One way) Overview of ANOVA General principle of ANOVA Variance decomposition Total Sum of Squares, Factorial and Residual sums of Squares. A purely geometrical step. Distributions of the Sums of Squares Sums of Squares as random variables. Distributions, independence. Properties as estimators of the common variance. ANOVA's F test ANOVA is a F test. Dunnett's test Dunnett's test Comparing group means to the mean of a reference group. t-test What are t-tests ? Is a sample average trustworthy ? One-sample t-test Is the sample mean significantly different from expected ? Student's t Distribution of the mean when the variance is unknown "Two dependent samples" t-test Are the means of 2 dependent samples equal ? "Two Independent samples" t-test Are the means of 2 independent samples equal ? t-test results How do I read software results of t-tests ? Chi-square tests The basic Chi-square test Does a sample match a multinomial distribution ? Continuous reference distribution Adapting the test to a continuous variable Estimated parameters If some parameters of the reference distribution are unknown The Chi-square test of equality Do several samples originate from the same distribution ? The Chi-square test of independence Are two categorical variables independent ? Complements on the Chi-square of independence Largest value, contributions, alternate coefficients. The Fisher-Irwin test The Fisher-Irwin test Are these two coins identically biased ? The Kolmogorov-Smirnov test The Kolmogorov statistic Its definition, distribution function, and the ensuing test. Complements on the Kolmogorov test Very short on : K-test or Chi-2 test ? Estimated parameters. Normality test. The Mann-Whitney test The Mann-Whitney statistic Its definition, distribution function, and the ensuing test. Complements on the Mann-Whitney test Very short on : Why ranks ? Location-shift test. Newman-Keuls test The Newman-Keuls test Pairwise comparisons of group means that avoid "paradoxical" conclusions.

Classification

Fisher's linear discriminant Fisher's criterion and Fisher's vector Definition and justification of Fisher's criterion. Maximizing Fisher's criterion (2 classes). Fisher's discriminant. Maximizing the generalized Fisher's criterion Maximizing the ratio of two quadratic forms. Maximizing the generalized Fisher's criterion. Discriminant Analysis What is Discriminant Analysis ? The most basic classification technique. Discriminant Function Analysis Finding new variables that are good at separating classes. Building a classifier Creating linear or quadratic Classification Functions. Complements on DA Just a little bit of maths. Logistic Regression What is Logistic Regression ? LR is a powerful generalization of Discriminant Analysis. What is the "logit" ? The information needed to build a score. Linear logit beyond DA Getting rid of the normality assumption. Estimating the coefficients of the model Likelihood, and how it is maximized. Decision Trees What are Decision Trees ? Heuristic, yet powerful classifiers. Can do Regression too. Growing a Tree Node splitting, Tree growth and Tree use. Three types of predictors Handling categorical, ordinal and numerical predictors Splitting a node Misclassification, Gini index, Entropy, Chi-square, Twoing Priors and costs Weighting the observations to favorably bias the Tree. Stopping rules and Pruning Getting the right size Tree to avoid overfitting

Exploratory Data Analysis

Principal Components Analysis (PCA) What is PCA ? An optimal way to display data on a plane, and more. What are Principal Components The most efficient synthetic variables for representing data. Finding the Principal Components Maximizing the inertia of projected observations. Projection of the observations The best projection of data on a plane. Projection of the variables Visualizing correlation between variables. Interpreting PCA results Interpreting the Principal Components and data distribution. Other applications of PCA Data Compression and Dimensionality reduction. Correspondence Analysis Overview of Correspondence Analysis Visualizing the interaction of two categorical variables. Reformating data Contengency tables, frequencies, profiles. The Chi-square distance ...is more appropriate than euclidian distance. The two PCAs How many dimensions, barycenters, total inertia. General principles of interpretation of CA Factors, weights, inertias, plots, quality of representation. Complete treatment of a real case A simple example from A to Z Complete treatment of a real case (1) Interpreting the inertia, the Chi-square, the factors. Complete treatment of a real case (2) Interpreting the plot of modalities for each variable. Complete treatment of a real case (3) Interpreting the combined plot of modalities. Complements on CA Supplementary variables, ordinal variables, Guttman effect.

Basic Concepts: Preorder, Partial Order, Total Order, Supremum

1) Total Order: a total order, linear order, simple order, or (non-strict) ordering on a set X is any binary relation on X that is antisymmetric, transitive, and total. This means that if we denote one such relation by ≤ then the following statements hold for all a, b and c in X:

if a ≤ b and b ≤ a then a = b (antisymmetry)

if a ≤ b and b ≤ c then a ≤ c (transitivity)

a ≤ b or b ≤ a (totality or completeness)

A set paired with an associated total order on it is called a totally ordered set, a linearly ordered set, a simply ordered set, or a chain.

2) Partial Order: is a binary relation "≤" over a set P which is reflexive, antisymmetric, and transitive, i.e., for all a, b, and c in P, we have that:

• a ≤ a (reflexivity);
• if a ≤ b and b ≤ a then a = b (antisymmetry);
• if a ≤ b and b ≤ c then a ≤ c (transitivity).

In other words, a partial order is an antisymmetric preorder.

A set with a partial order is called a partially ordered set (also called a poset).

3) Preorder: Consider some set P and a binary relation on P. Then is a preorder, or quasiorder, if it is reflexive and transitive, i.e., for all a, b and c in P, we have that:

a a (reflexivity)

if a b and b c then a c (transitivity)

A set that is equipped with a preorder is called a preordered set.

If a preorder is also antisymmetric, that is, a b and b a implies a = b, then it is a partial order. In that case there is no need for the special symbol and we can just write ≤.

On the other hand, if it is symmetric, that is, if a b implies b a, then it is an equivalence relation.

4) Supremum: given a subset S of a partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to each element of S. Consequently, the supremum is also referred to as the least upper bound, lub or LUB. If the supremum exists, it may or may not belong to S. If the supremum exists, it is unique.