In principle, ρ is simply a special case of the Pearson product-moment coefficient in which the data are converted to rankings before calculating the coefficient. In practice, however, a simpler procedure is normally used to calculate ρ. The raw scores are converted to ranks, and the differences d between the ranks of each observation on the two variables are calculated.
If there are no tied ranks, i.e. 
then ρ is given by:
where:
- di = the difference between each rank of corresponding values of x and y, and
- n = the number of pairs of values.
If tied ranks exist, classic Pearson's correlation coefficient between ranks has to be used instead of this formula. You have to assign the same rank to each of the equal values. It is an average of their positions in the ascending order of the values:
An Example of Averaging Ranks
| Variable | Position in the decending order | Rank |
|---|---|---|
| 0.8 | 5 | 5 |
| 1.2 | 4 |  |
| 1.2 | 3 |  |
| 2.3 | 2 | 2 |
| 18 | 1 | 1 |
Spearman's rank correlation coefficient is equivalent to Pearson correlation on ranks. The formula above is a short-cut to its product-moment form, assuming no tie. The product-moment form can be used in both tied and untied cases.
A version of this correlation is called Spearman's rho. In this case ranks are calculated as above, but in the formula of Pearson's correlation a standard deviation is taken as there were no ties.
Another popular method for computing rank correlation is the Kendall tau rank correlation coefficient.
Example
The raw data used in this example is shown below.
| IQ | Hours of TV per week. |
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
The first step is to sort this data by the first column. Next, two more columns are created. Both of these are for ranking the first two columns. Notice how the rank of values that are the same is the mean of what their ranks would otherwise be. Then a column "d" is created to hold the differences between the two rank columns. Finally another column "d2" should be created. This is just column d squared.
After doing this process with the example data you should end up with something like:
| IQ (i) | Hours of TV per week (t) | rank (i) | rank (t) | d | d2 |
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | 4 | 16 |
| 99 | 28 | 3 | 8 | 5 | 25 |
| 100 | 27 | 4 | 7 | 3 | 9 |
| 101 | 50 | 5 | 10 | 5 | 25 |
| 103 | 29 | 6 | 9 | 3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
The values in the d2 column can now be added to find  . The value of n is 10. So these values can now be substituted back into the equation,
. The value of n is 10. So these values can now be substituted back into the equation,
which evaluates to ρ = − 0.175758. In the case of ties in the original values, then this formula should not be used. Instead, the Pearson correlation coefficient should be calculated on the ranks (where ties are given ranks, as described above).
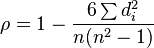
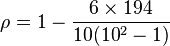
No comments:
Post a Comment