Johnny Deng's Column: Correlation ratio

In statistics, the correlation ratio is a measure of the relationship between the statistical dispersion within individual categories and the dispersion across the whole population or sample.

Suppose each observation is y_xi where x indicates the category that observation is in and i is the label of the particular observation. We will write n_x for the number of observations in category x (not necessarily the same for different values of x) and

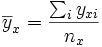$\overline{y}_x=\frac{\sum_i y_{xi}}{n_x}$ and $\overline{y}=\frac{\sum_x n_x \overline{y}_x}{\sum_x n_x}$

then the correlation ratio η (eta) is defined so as to satisfy

$\eta^2 = \frac{\sum_x n_x (\overline{y}_x-\overline{y})^2}{\sum_{xi} (y_{xi}-\overline{y})^2}$

which might be written as

$\frac{{\sigma_{\overline{y}}}^2}{{\sigma_{y}}^2}.$

It is worth noting that if the relationship between values of $x \;\$ and values of $\overline{y}_x$ is linear (which is certainly true when there are only two possibilities for x) this will give the same result as the square of the correlation coefficient; if not then the correlation ratio will be larger in magnitude, though still no more than 1 in magnitude. It can therefore be used for judging non-linear relationships.

Retrieved from "http://en.wikipedia.org/wiki/Correlation_ratio"

Johnny Deng's Column

Saturday, 1 September 2007

Correlation ratio

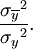
No comments:

Site Search

Blog Archive

Who am I?

Access History