Linear function
In mathematics, the term linear function can refer to either of two different but related concepts.
Usage in elementary mathematics
In elementary algebra and analytic geometry, the term linear function is often used to mean a first degree polynomial function of one variable. These functions are called "linear" because they are precisely the functions whose graph in the Cartesian coordinate plane is a straight line.
Such a function can be written as
- f(x) = mx + b,
where m and b are real constants and x is a real variable. The constant m is often called the slope while b is the y-intercept, which gives the point of intersection between the graph of the function and the y-axis. Changing m makes the line steeper or shallower, while changing b moves the line up or down.
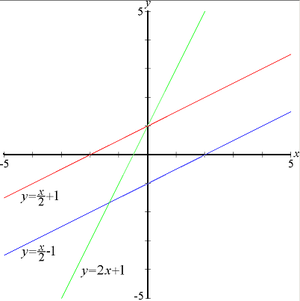
Examples of functions whose graph is a line include the following:
- f1(x) = 2x + 1
- f2(x) = x / 2 + 1
- f3(x) = x / 2 − 1
The graphs of these are shown in the image at right.
Usage in advanced mathematics
In advanced mathematics, a linear function often means a function that is a linear map, that is, a map between two vector spaces that preserves vector addition and scalar multiplication.
A function f(x) = mx + b is a linear map if and only if b = 0. For other values of b this falls in the more general class of affine maps.
1 comment:
A new nonhomogeneous system, which is linear apart from the presence of a function of the independent variables, is nonlinear as outlined by a strict explanation, but such systems tend to be studied alongside linear techniques, because they may be transformed to some sort of linear system of multiple variables.pre algebra practice
Post a Comment