Information and Entropy

by Johnny.Deng

Bits as Information Media: Information is carried by bits. Generally, if there are n outcomes for information, log2(n) bits are needed to express the information (may be more). That is also to say: Base-2 logarithms information is expressed in bits.

Information: Based on above, but more exactly, the information learned from outcomes of event Ai in an event space should be log2(1/P(Ai)), in which P(Ai) is the propability of the outcome of event Ai. Note from this formula that if p(Ai) = 1 for some i, then the information learned from that outcome is 0 since log2(1) = 0. This is consistent with what we would expect. The less frequently the event happens, the more information it carries.

Entropy: The average information per event is found by multiplying the information for each event Ai by p(Ai) and summing over the partition:, which is called Entropy.

Both of the concepts are based on Statistical Probability of outcome of events, which represents the uncertainty of Information, i.e. a lack of information.

An application of above theory is soure encoding:

What we need from the source encoding in comunication between senders and recievers is to get as compressed information as possible considering efficiency. However, if a source has n possible symbols (A) based on the outcome probablily, P(Ai), respecitively, the least or compressed average bits for each symbols of the source should be , i.e. the least entropy contained in the code is most effective. Otherwise, note that bits denote information, least bits reduced uncertainty of information.
For example:In a typical course with good students, the grade distribution might be:
A B C D F
25% 50% 12.5% 10% 2.5%
Assuming this as a probability distribution, what is the information per symbol and what is the average information per symbol?


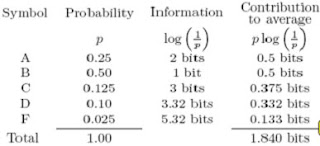
Here goes the minimum average information per symbol, 1.840 bits, ideally, comparing with the pratically best coding algorithem: Huffman Code, which is as follows:


The avearage coded length is 1.875, greater than the theoretically average information per symbol, 1.840, because the symbols D and F cannot be encoded in fractional bits. If a block of several symbols were considered together, the average length of the Huffman code could be closer to the actual information per symbol, but not below it. By the way, the “block coding” is a little tricky that we group the symbols in blocks per sending in case of redundency of bits in stead of sending one symbol each time.